Distribución Normal
La distribución normal, también conocida como distribución gaussiana o curva de campana es fundamental en Estadística|estadística moderna. Su omnipresencia en fenómenos naturales y artificiales la convierte en una herramienta indispensable .
Definición Matemática
La distribución normal se define mediante su función de densidad de probabilidad:
$$f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}$$
Donde:
- $\mu$ representa la media de la distribución
- $\sigma$ representa la desviación estándar
- $e$ es la base del logaritmo natural
- $\pi$ es la constante matemática pi
Esta ecuación genera la característica curva en forma de campana simétrica alrededor de su media.
Propiedades Fundamentales
La distribución normal posee varias propiedades que la hacen matemáticamente elegante y prácticamente útil:
-
Simetría: Es perfectamente simétrica alrededor de su media, lo que implica que la media, mediana y moda coinciden exactamente.
-
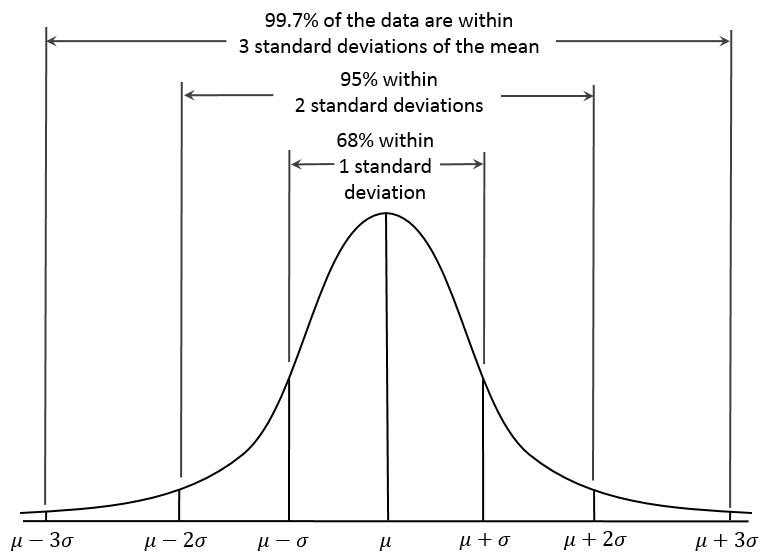
La regla 68-95-99.7: También conocida como la regla empírica:
- Aproximadamente el 68% de los datos se encuentran dentro de una desviación estándar de la media ($\mu \pm \sigma$)
- Aproximadamente el 95% dentro de dos desviaciones estándar ($\mu \pm 2\sigma$)
- Aproximadamente el 99.7% dentro de tres desviaciones estándar ($\mu \pm 3\sigma$)
- Distribución Estándar: Cualquier distribución normal puede transformarse en la distribución normal estándar (con $\mu=0$ y $\sigma=1$) mediante la estandarización: $$z = \frac{x-\mu}{\sigma}$$
-
Aditividad: La suma de variables aleatorias normales independientes es también una variable aleatoria normal.
Regla empírica
Importancia Histórica
La distribución normal fue inicialmente desarrollada por Abraham de Moivre en 1733, pero ganó reconocimiento cuando Carl Friedrich Gauss la utilizó para analizar errores en mediciones astronómicas. El nombre "gaussiana" hace honor a su contribución.
Gauss descubrió que los errores pequeños ocurrían con mayor frecuencia que los grandes, y que estos errores se distribuían simétricamente alrededor del valor verdadero. Esta observación fue crucial para el desarrollo del método de mínimos cuadrados y sentó las bases para gran parte de la estadística moderna.
Aplicaciones Prácticas
La distribución normal encuentra aplicaciones en numerosos campos:
Análisis de Datos
- Inferencia estadística: Muchas pruebas estadísticas asumen normalidad en los datos.
- Intervalos de confianza: Construcción de rangos que probablemente contengan el valor verdadero de un parámetro.
Control de Calidad
- Límites de control: Establecimiento de umbrales para detectar anomalías en procesos industriales.
- Capacidad de proceso: Evaluación de la habilidad de un proceso para cumplir especificaciones.
Ciencias Naturales
- Errores de medición: En física y otras ciencias, los errores instrumentales suelen seguir distribuciones normales.
- Fenómenos biológicos: Desde alturas humanas hasta características morfológicas en especies.
Finanzas
- Modelos de riesgo: Base para el análisis de volatilidad y estimación de riesgos.
- Teoría de portafolios: Fundamento para la optimización de inversiones.
Limitaciones y Consideraciones
A pesar de su utilidad, es crucial reconocer cuándo la distribución normal puede no ser apropiada:
-
Datos acotados: La distribución normal abarca desde $-\infty$ hasta $+\infty$, lo que puede no ser realista para variables con límites naturales.
-
Asimetría: Muchos fenómenos reales presentan asimetría (skewness), como tiempos de respuesta en sistemas informáticos o distribuciones de ingresos.
-
Colas pesadas: Algunos datos exhiben "colas pesadas" (más valores extremos que los predichos por la normal), como en mercados financieros durante crisis.
-
Muestras pequeñas: La aproximación normal puede ser inexacta con tamaños de muestra reducidos.
Pruebas de Normalidad
Para verificar si un conjunto de datos sigue una distribución normal, existen diversas pruebas:
- Gráficos Q-Q: Comparan cuantiles teóricos con los observados.
- Prueba de Shapiro-Wilk: Evalúa estadísticamente la hipótesis de normalidad.
- Prueba de Anderson-Darling: Sensible especialmente a las desviaciones en las colas.