Jerarquía de Chomsky
Definen los Lenguajes Formales según la complejidad de su Gramática (Autómata):
- Gramáticas de estructura de frase
- Gramáticas dependientes del contexto
- Gramática Independiente del Contexto
- Gramática Regular
Los tipos de gramáticas anteriores cumplen la relación de inclusión mostrada en la siguiente figura:
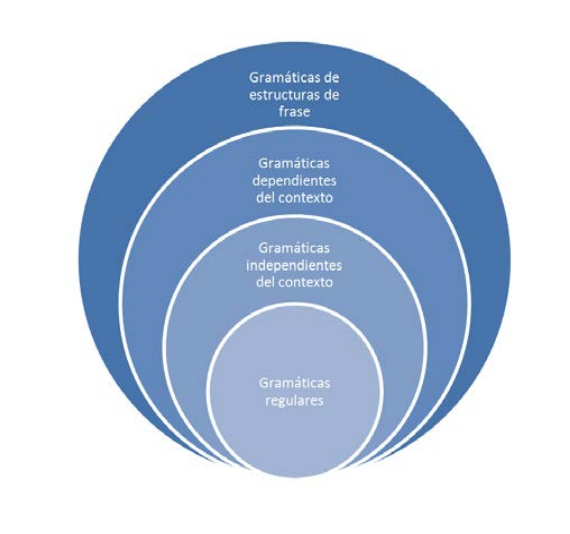
Como puede observarse, desde las gramáticas de estructura de frase hasta las regulares, cada tipo incluye el siguiente, y forman una relación jerárquica. De aquí el nombre de jerarquía de Chomsky para este conjunto de clases de gramáticas.
| Tipo de Gramática | Lenguajes | Autómata Reconocedor | Reglas de Producción (Restricciones) | Ejemplos |
|---|---|---|---|---|
| Tipo-3 | Regulares | Autómatas finitos Finito | - (A $\to$ a) (regular derecha) - (A $\to$ aB) o - (A $\to$ a) (regular izquierda) - (A $\to$ Ba) |
(L = {$a^n \mid n > 0$}) |
| Tipo-2 | Independientes del Contexto | Autómata de Pila | ($A \to \alpha$) | (L = {$a^n b^n \mid n$ > 0}) |
| Tipo-1 | Sensibles al Contexto | Máquina de Turing No Determinista Acotada Linealmente | ($\alpha A \beta \to \alpha \gamma \beta$) | (L = {$a^n b^n c^n \mid n > 0$}) |
| Tipo-0 | Recursivamente Enumerables | Máquina de Turing | ($\gamma \to \alpha$) ($\gamma) no vacío$) | (L = {w $\mid$ w describe una máquina de Turing que termina}}) |
| De las subclases mencionadas, las gramáticas regulares constituyen los modelos generadores de lenguajes regulares que, junto al modelo declarativo (expresiones regulares) y a los modelos reconocedores (autómatas finitos deterministas y no deterministas), permiten representar y estudiar los lenguajes regulares. |
[!note] Relación biunívoca La relación biunívoca anterior significa es relación uno a uno, para toda gramática hay un solo autómata que la reconoce y viceversa.
Por ejemplo: - Si tenemos una gramática de estructura de frase cualquiera, existe entonces una máquina de Turing que acepta el mismo lenguaje que el generado por la gramática - Si tenemos una máquina de Turing cualquiera, existe entonces una gramática de estructura de frase que genera el mismo lenguaje que el aceptado por la máquina de Turing