Analizar sintáctico LL(k)
Un analizador LL(k) es un Analizador sintáctico descendente circunscrito a una Gramática Independiente del Contexto. Generalmente se usan para analizar Lenguajes de programación]]. En este analizador las entradas son de izquierda a derecha, y construcciones de derivaciones por la izquierda de una sentencia o enunciado. La clase de gramática que es analizable por este método es conocido como gramática LL.
En un analizador LL(k) se usan K tokens, es decir se tienen que conocer un número K de caracteres delante de la actual posición de análisis, sin ir hacia atrás. La más popular es la LL(1) que solo necesita conocer un caracter hacia delante.
Estos analizadores se distinguen de un Autómatas con pila por tres aspectos: - el control se hace mediante una tabla (y no por estados) - el apuntador del control no se pasa al próximo símbolo tras conocer su valor, sino que se mantiene hasta que se asegura que es el terminal correcto en ese momento. - Durante el proceso de análisis se emite como salida la sucesión de reglas aplicadas que corresponden al análisis descendente de la cadena procesa.
Una gramática analizable por LL(1), en adelante gramática LL(1) require tres condiciones:
- no debe tener recursión por la izquierda como por ejemplo la regla A -> Ab.
- la gramática no debe tener ambigüedades.
- se debe factorizar por la izquierda para hacer la gramática determinística.
Ejemplo de indeterminación en una gramática
Sea la gramática:
$G = { S \to bS \;|\; aA, \; A \to aA \;|\; aB \;|\; a, \; B \to bO \;|\; b }$
Analizamos la palabra aab:
-
Desde ( S ):
Aplicamos ( S $\to$ aA ), obteniendo aA. -
Ahora, al derivar $( A )$, surgen dos opciones posibles:
- ( A \$to$ aA ), lo que genera aaA.
- ( A $\to$ aB ), lo que genera aaB.
Esto produce una indeterminación porque no hay un criterio claro para decidir qué regla aplicar. En este caso, la gramática no es LL(1) porque tiene reglas con prefijos comunes (( aA ) y ( aB )) que generan ambigüedad en el análisis.
Tecnica LL(1)
Ejemplo de Tabla de Control
Supongamos la gramática:
$G = { S \to aA \;|\; bB, \; A \to aA \;|\; a, \; B \to bB \;|\; b }$
La tabla de control LL(1) sería:
$$ \begin{array}{|c|c|c|c|} \hline & a & b & \$ \ \hline S & S \to aA & S \to bB & \text{Error} \ A & A \to aA & \text{Error} & A \to a \ B & \text{Error} & B \to bB & B \to b \ \hline \end{array} $$
El procesador al iniciar el análisis se encuentra en esta configuración:
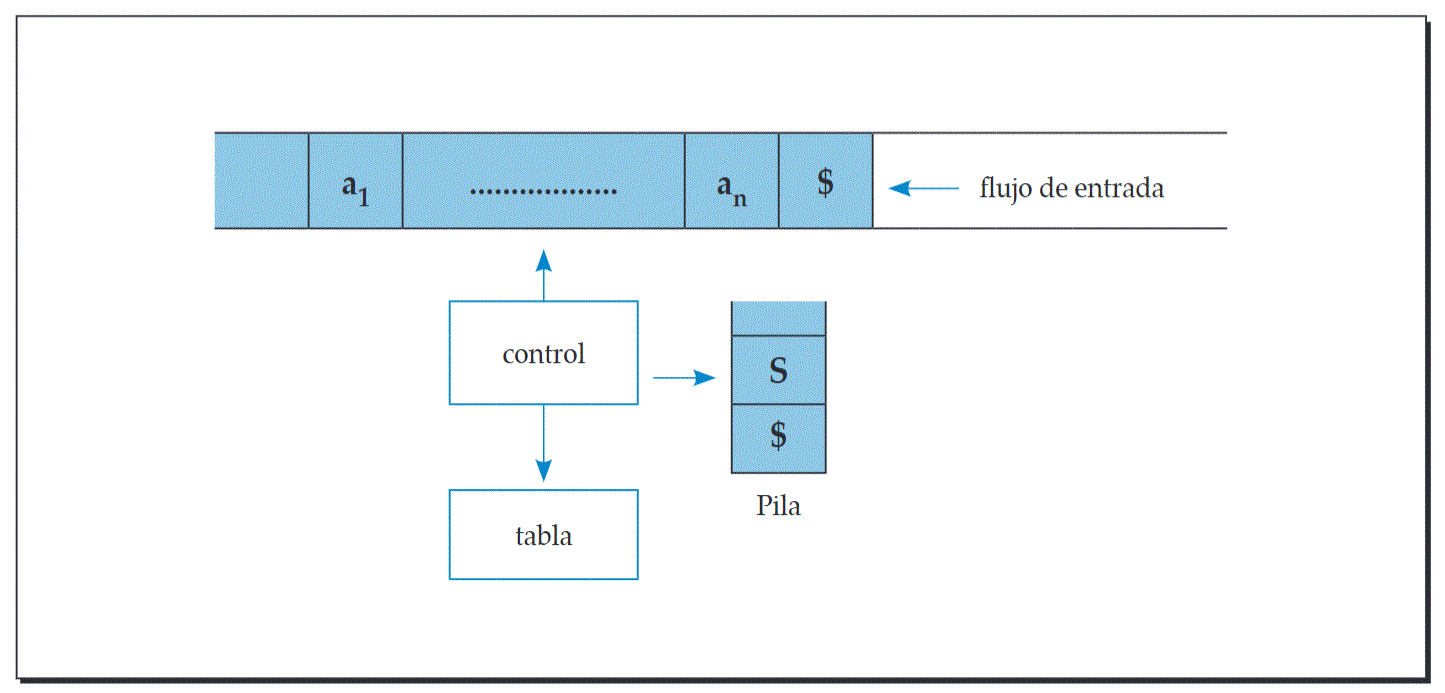
Reglas de Aplicación
flowchart TD
A[Inicio: Cadena de Entrada] --> B{¿Pila Vacía?}
B -->|Sí| C[Éxito: Cadena Aceptada]
B -->|No| D{¿Tope es Terminal?}
D -->|Sí| E{¿Coincide con entrada?}
E -->|Sí| F[Hacer Pop en Pila y\nAvanzar Entrada]
E -->|No| G[Error: Terminal\nno coincide]
D -->|No| H{¿Existe en Tabla LL1?}
H -->|Sí| I[Aplicar Producción\nde Tabla LL1]
H -->|No| J[Error: No hay\nproducción válida]
F --> B
I --> B
G --> K[Rechazar Entrada]
J --> K
style A fill:#f9f,stroke:#333,stroke-width:2px
style C fill:#9f9,stroke:#333,stroke-width:2px
style K fill:#f99,stroke:#333,stroke-width:2px
style G fill:#fcc,stroke:#333
style J fill:#fcc,stroke:#333
```- Si la cima de la pila es un no terminal, sustituirlo por su derivación en la cima de la pila:
- Busca en la tabla la fila correspondiente a (X) y la columna del símbolo actual de entrada (a).
- Si hay una regla ($X \to \alpha$), quita (X) de la pila y mete ($\alpha$) en su lugar.
-
Si no hay regla, es un error.
-
Si la cima de la pila es un terminal (a):
- Compara el símbolo en la cima de la pila con el símbolo actual de la entrada.
- Si coinciden, quítalo de la pila y avanza al siguiente símbolo de entrada.
-
Si no coinciden, es un error.
-
Si la cima de la pila es el símbolo de fin ($):
- Si tanto la pila como la entrada tienen el símbolo (\$), el análisis terminó con éxito.
- Si no coinciden, es un error.
Ejemplo de Uso
Entrada: aab
Pila inicial: (S\$)
1. Aplicamos la regla (S $\to$ aA). Pila: (aA\$).
2. Comparamos \(a\) (pila) con \(a\) (entrada), coinciden. Avanzamos: Pila: \(A\$\), Entrada: **ab**.
3. Aplicamos \(A $\to$ aA\). Pila: \(aA\$\).
4. Comparamos \(a\) (pila) con \(a\) (entrada), coinciden. Avanzamos: Pila: \(A\$\), Entrada: **b**.
5. Aplicamos \(A $\to$ a\). Pila: \(a\$\).
6. Comparamos \(a\) (pila) con \(a\) (entrada), coinciden. Avanzamos: Pila: \(\$\), Entrada: \(\$\).
¡Análisis exitoso!